Vector flow

In mathematics, the vector flow refers to a set of closely related concepts of the flow determined by a vector field. These appear in a number of different contexts, including differential topology, Riemannian geometry and Lie group theory. These related concepts are explored in a spectrum of articles:

Vector flow in differential topology

Relevant concepts: (flow, infinitesimal generator, integral curve, complete vector field)

Let V be a smooth vector field on a smooth manifold M. There is a unique maximal flow D → M whose infinitesimal generator is V. Here D ⊆ R × M is the flow domain. For each p ∈ M the map Dp → M is the unique maximal integral curve of V starting at p.

A global flow is one whose flow domain is all of R × M. Global flows define smooth actions of R on M. A vector field is complete if it generates a global flow. Every vector field on a compact manifold without boundary is complete.

Vector flow in Riemannian geometry

Relevant concepts: (geodesic, exponential map, injectivity radius)

The exponential map

exp : TpM → M

is defined as exp(X) = γ(1) where γ : I → M is the unique geodesic passing through p at 0 and whose tangent vector at 0 is X. Here I is the maximal open interval of R for which the geodesic is defined.

Let M be a pseudo-Riemannian manifold (or any manifold with an affine connection) and let p be a point in M. Then for every V in TpM there exists a unique geodesic γ : I → M for which γ(0) = p and 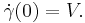\dot\gamma(0) = V. Let Dp be the subset of TpM for which 1 lies in I.

Vector flow in Lie group theory

Relevant concepts: (exponential map, infinitesimal generator, one-parameter group)

Every left-invariant vector field on a Lie group is complete. The integral curve starting at the identity is a one-parameter subgroup of G. There are one-to-one correspondences

{one-parameter subgroups of G} ⇔ {left-invariant vector fields on G} ⇔ g = TeG.

Let G be a Lie group and g its Lie algebra. The exponential map is a map exp : g → G given by exp(X) = γ(1) where γ is the integral curve starting at the identity in G generated by X.